Maths revision week 1 to 12

Course Summary

📚

Course Summary

For Stats 1 summary click here.

For English 1 summary click here.

For Qualifier exam click here.

Week 1 to 4 (Qualifier)

Week 1: Relations and Venn Diagrams

In the first week, we focused on understanding different types of relations: reflexive, symmetric, transitive, and equivalence relations. We also explored the use of Venn diagrams to solve problems involving sets.

Important Concepts:

Reflexive Relation: A relation $ R $ on a set $ A $ is reflexive if $ \forall a \in A, (a, a) \in R $.
Symmetric Relation: A relation $ R $ on a set $ A $ is symmetric if $ \forall a, b \in A, (a, b) \in R \implies (b, a) \in R $.
Transitive Relation: A relation $ R $ on a set $ A $ is transitive if $ \forall a, b, c \in A, (a, b) \in R \land (b, c) \in R \implies (a, c) \in R $.
Equivalence Relation: A relation that is reflexive, symmetric, and transitive.

Venn Diagram Formula:

$$|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B|$$

$$- |A \cap C| - |B \cap C| + |A \cap B \cap C|$$

Example:

Suppose we have three groups of people: those who like football, hockey, and cricket. Let:

$ |A| = 30 $ (football)
$ |B| = 25 $ (hockey)
$ |C| = 20 $ (cricket)
$ |A \cap B| = 10 $
$ |A \cap C| = 5 $
$ |B \cap C| = 8 $
$ |A \cap B \cap C| = 3 $

Using the formula, the number of people who like exactly one sport is: \[ |A \cup B \cup C| = 30 + 25 + 20 - 10 - 5 - 8 + 3 = 55 \]

Week 2: Lines and Distance

This week, we covered various geometric concepts related to lines and distances.

Important Concepts:

Midpoint Formula: The midpoint of a line segment with endpoints $(x_1, y_1)$ and $(x_2, y_2)$ is: \[ \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]
Distance Formula: The distance between two points $(x_1, y_1)$ and $(x_2, y_2)$ is: \[ \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \]
Equation of a Line: The general form is $Ax + By + C = 0$.
Distance Between Two Parallel Lines: The distance between $Ax + By + C_1 = 0$ and $Ax + By + C_2 = 0$ is: \[ \frac{|C_2 - C_1|}{\sqrt{A^2 + B^2}} \]
Sum of Squared Errors: A measure used in regression analysis to determine the accuracy of a model.

Week 3: Quadratic Functions

We delved into quadratic functions, their properties, and their graphs.

Important Concepts:

Quadratic Function: A function of the form $f(x) = ax^2 + bx + c$.
Vertex: The highest or lowest point on the graph of a parabola, given by: \[ \left( -\frac{b}{2a}, f\left( -\frac{b}{2a} \right) \right) \]
Discriminant: Determines the nature of the roots of a quadratic equation $ax^2 + bx + c = 0$, given by: \[ \Delta = b^2 - 4ac \]

Week 4: Polynomials

This week, we explored polynomials and their properties.

Important Concepts:

Zeros of a Polynomial: The values of $x$ for which $P(x) = 0$.
Factors of a Polynomial: Expressions that can be multiplied to get the polynomial.
Intercepts: Points where the graph intersects the axes.
Multiplicity of Roots: The number of times a particular root appears.
End Behavior: The behavior of the graph as $x$ approaches $\pm \infty$.
Turning Points: Points where the graph changes direction.

Mid-Term Focus (Weeks 5 to 8)

For the mid-term quiz, more weightage will be given to topics from weeks 5 to 8, but questions from weeks 1 to 4 will also be included.

Week 5: Functions

We studied different types of functions and their compositions.

Important Concepts:

One-to-One Function: A function where each element of the range is mapped to by exactly one element of the domain.
Onto Function: A function where every element of the range is mapped to by at least one element of the domain.
Composition of Functions: Combining two functions $f$ and $g$ to form $f(g(x))$.

Week 6: Logarithmic Functions

This week, we focused on logarithmic functions and their properties.

Important Concepts:

Logarithmic Function: The inverse of an exponential function, given by $y = \log_b(x)$.
Properties of Logarithms: \[ \log_b(xy) = \log_b(x) + \log_b(y) \] \[ \log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y) \] \[ \log_b(x^y) = y \log_b(x) \]
Concept of Limits: Understanding the behavior of functions as they approach specific points.
L'Hôpital's Rule: A method to evaluate limits of indeterminate forms: \[ \lim_{x \to c} \frac{f(x)}{g(x)} = \lim_{x \to c} \frac{f'(x)}{g'(x)} \]

Week 8: Continuity and Differentiability

In Week 8, we focused on the concepts of continuity and differentiability, which are fundamental in calculus.

Continuity:

A function $ f(x) $ is continuous at a point $ x = a $ if the following three conditions are met:

$ f(a) $ is defined.
$ \lim_{x \to a} f(x) $ exists.
$ \lim_{x \to a} f(x) = f(a) $.

This means there are no breaks, jumps, or holes in the graph of the function at $ x = a $.

Differentiability: A function $ f(x) $ is differentiable at a point $ x = a $ if the derivative $ f'(a) $ exists. This implies that the function is smooth and has no sharp corners or cusps at $ x = a $.

Equation of Tangent and Linear Approximation

Equation of Tangent: The equation of the tangent line to the curve $ y = f(x) $ at the point $ (a, f(a)) $ is given by: \[ y - f(a) = f'(a)(x - a) \] This line touches the curve at exactly one point and has the same slope as the curve at that point.

Linear Approximation: Linear approximation is used to approximate the value of a function near a given point. The linear approximation of $ f(x) $ near $ x = a $ is: \[ f(x) \approx f(a) + f'(a)(x - a) \] This is essentially the equation of the tangent line and provides a good approximation for values of $ x $ close to $ a $.

End-Term Focus: Graph Theory

Question will be from week 1 to 11

For the end-term exam, more weightage will be given to graph theory. Here are the key topics:

Week 9: Integration

Integration: Integration is the process of finding the integral of a function, which represents the area under the curve of the function. The definite integral of $ f(x) $ from $ a $ to $ b $ is given by: \[ \int_a^b f(x) \, dx \]

Riemann Sum: The Riemann sum is a method for approximating the definite integral of a function. It involves dividing the interval $[a, b]$ into smaller subintervals and summing up the areas of rectangles formed by the function values at specific points within the subintervals.

Graph Theory

Breadth-First Search (BFS) and Depth-First Search (DFS): BFS and DFS are fundamental algorithms for traversing graphs. BFS explores all neighbors of a vertex before moving on to the next level, while DFS explores as far as possible along each branch before backtracking.

Directed Acyclic Graph (DAG): A DAG is a directed graph with no cycles. It is important for representing tasks with dependencies.

Topological Sorting: Topological sorting is used to order the vertices of a DAG such that for every directed edge $ uv $, vertex $ u $ comes before $ v $. This is crucial for scheduling tasks.

Longest Path in DAG: Finding the longest path in a DAG is important for determining the maximum time required to complete a sequence of tasks.

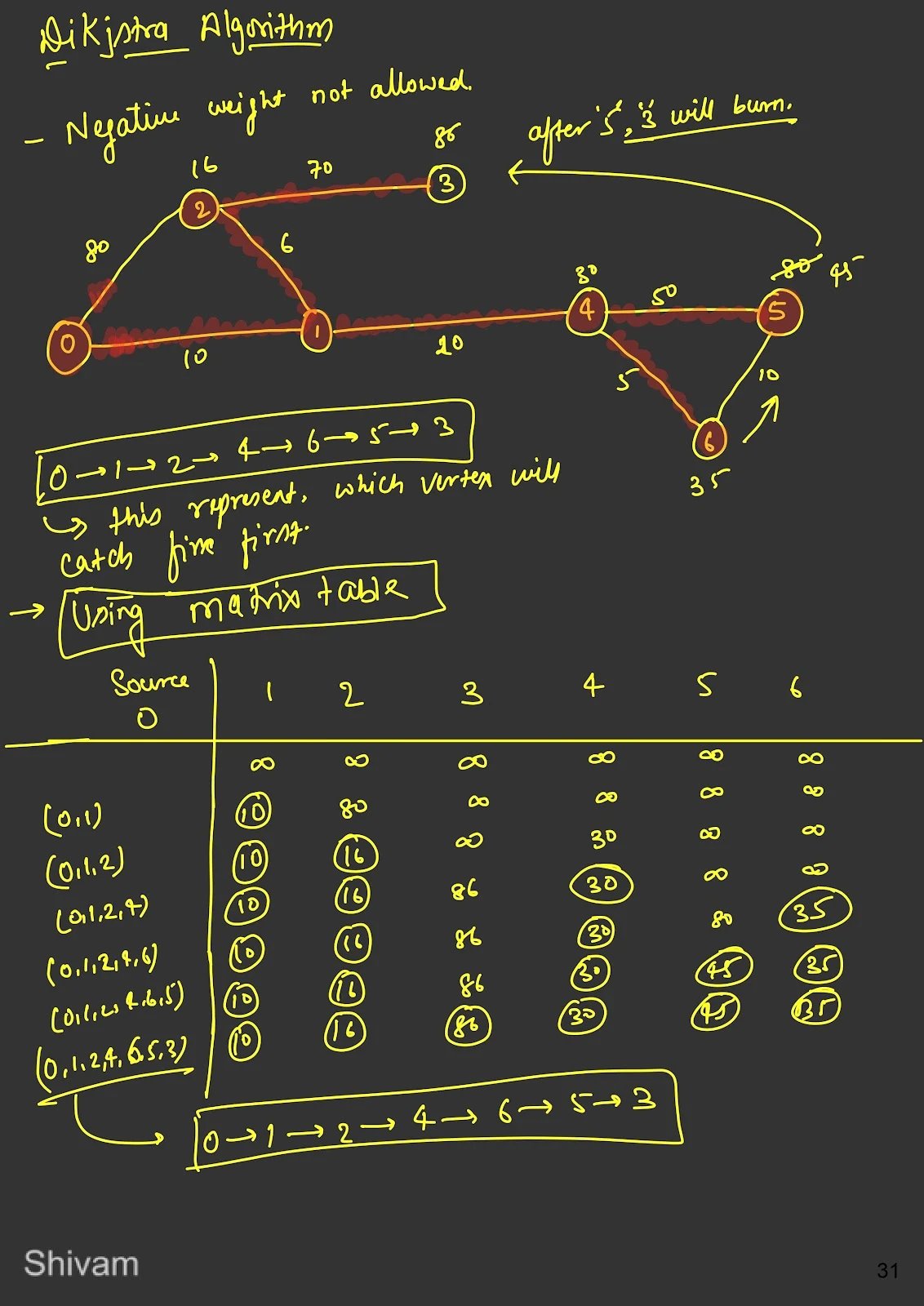
Dijkstra's Algorithm: Dijkstra's algorithm finds the shortest path from a source vertex to all other vertices in a graph with non-negative weights. It does not work with negative weights.

Bellman-Ford and Floyd-Warshall Algorithms: These algorithms handle graphs with negative weights but no negative cycles. Bellman-Ford works by iterating over all edges, while Floyd-Warshall considers all pairs of vertices.

Minimum Cost Spanning Tree (MCST): An MCST connects all vertices in a graph with the minimum total edge weight. Kruskal's and Prim's algorithms are used to find the MCST.

Kruskal's Algorithm: Kruskal's algorithm sorts all edges and adds them one by one to the spanning tree, ensuring no cycles are formed.

Prim's Algorithm: Prim's algorithm starts with a single vertex and grows the spanning tree by adding the smallest edge that connects a vertex in the tree to a vertex outside the tree.

Both algorithms yield the same MCST, and it's useful to cross-verify the results obtained from one algorithm with the other.