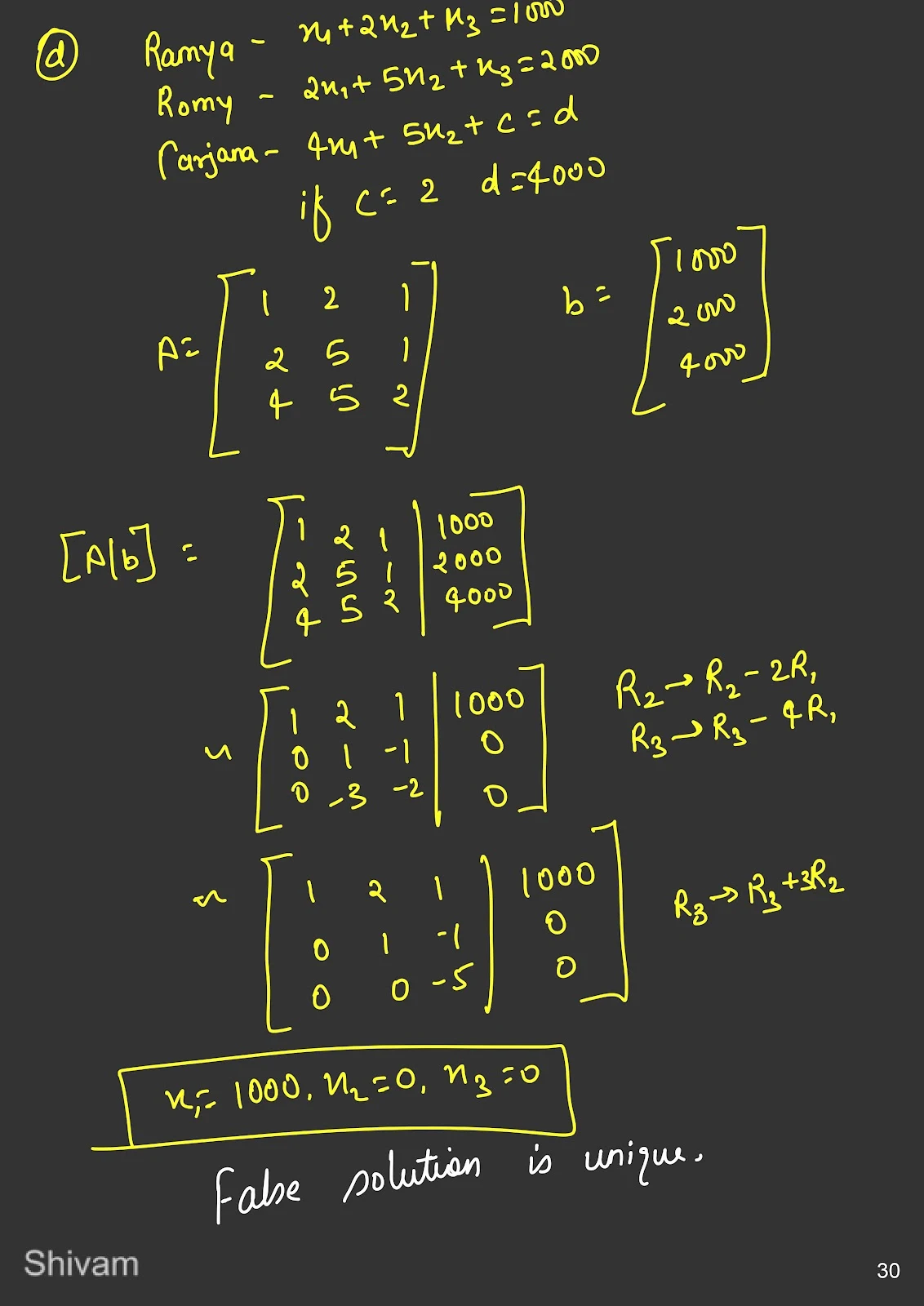--> Skip to main content
Please leave a comment below if you have any questions or suggestions!

Maths 2 Week 2

Linear Algebra Concepts and Solvers

πŸ“š

Minor, Cofactor, and Determinant

Minor: The minor of an element is the determinant of the matrix formed by deleting the row and column of that element.
Cofactor: The cofactor of an element \( a_{ij} \) is given by \( C_{ij} = (-1)^{i+j} M_{ij} \).
Determinant: The determinant is a scalar value representing certain properties of the matrix.

2x2 Determinant Formula:

For a 2x2 matrix \( A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \), the determinant is calculated as: \[ \text{det}(A) = ad - bc \]

πŸ‘‰Determinant Calculator

Cramer's Rule

Cramer's Rule is a method for solving a system of linear equations using determinants. For a system \( A \mathbf{x} = \mathbf{b} \), the solution for each variable is given by: \[ x_i = \frac{\text{det}(A_i)}{\text{det}(A)} \] where \( A_i \) is the matrix formed by replacing the \( i \)-th column of \( A \) with \( \mathbf{b} \).

Cramer's Rule Solver:

Enter constants:

Solution:

Inverse of a Matrix

The inverse of a matrix \( A \) is denoted as \( A^{-1} \), and it's defined as \( A A^{-1} = A^{-1} A = I \), where \( I \) is the identity matrix.
The inverse can be calculated using various methods, depending on the matrix size.

Matrix Size:

Inverse:

Rank of a Matrix

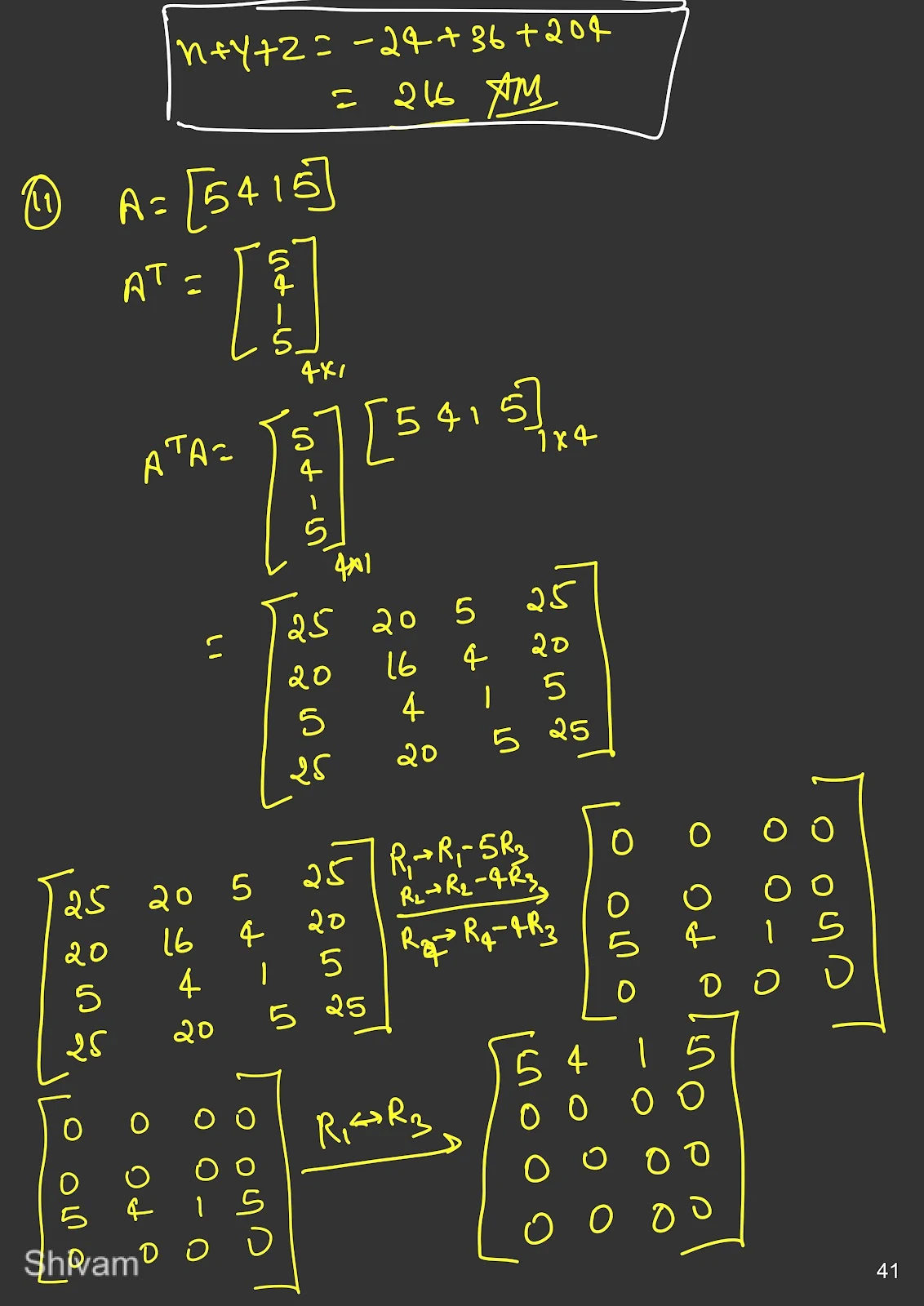
The rank of a matrix is the maximum number of linearly independent row or column vectors in the matrix. It can be calculated by transforming the matrix into its Row Echelon Form (REF) or Reduced Row Echelon Form (RREF).

Matrix Size:

Rank:

Row Echelon Form (REF)

The Row Echelon Form of a matrix is achieved when all nonzero rows are above any rows of all zeros, and the leading coefficient of a nonzero row is always to the right of the leading coefficient of the previous row.

Matrix Size:

Row Echelon Form:

Gauss Elimination Method

The Gauss elimination method is used to solve systems of linear equations. It involves using row operations to transform the system into an equivalent system that is easier to solve.

Matrix Size:

Enter constants:

Solution:

Comments

Post a Comment

Popular post

IITM Notes

Honoring Ratan Tata Please take a moment to read this tribute. (Click the box to view the full article) “These handwritten notes encompass topics in data science and civil services. The beauty of knowledge is that you don’t need to belong to any specific group; simply maintain your curiosity, and knowledge will find its way to you. I hope these notes are helpful. If they are, please consider leaving a comment below and follow my blog for updates.” “I’ve started a qualifier series where I’ll summarize maths and stats topics for the qualifier exam and discuss previous year questions (PYQs). Please subscribe to my YouTube channel for updates!” SUBSCRIBE Mathematics 1 πŸ‘‰ Select Week Week 1 Week 2 Week 3 Week 4 Week 5 Week 6 Week 7 Week 8 Week 9
7 comments
Click here to read more

Maths 1 Week 4 Summary

Polynomial Summary πŸ“š Polynomial Summary Polynomial A polynomial is an expression consisting of variables (also called indeterminates) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. For example, \(3x^2 + 2x - 5\) is a polynomial. Degree of Polynomial The degree of a polynomial is the highest power of the variable in the polynomial. For example, in the polynomial \(4x^3 + 3x^2 + 2x + 1\), the degree is 3. Multiplication of Polynomials To multiply two polynomials, each term in the first polynomial is multiplied by each term in the second polynomial. For example: \((2x + 3)(x - 4) = 2x \cdot x + 2x \cdot (-4) + 3 \cdot x + 3 \cdot (-4) = 2x^2 - 8x + 3x - 12 = 2x^2 - 5x - 12\) Division of Polynomials To divide polynomials, we use polynomial long division or synthetic division. For example, dividing \(2x^3 + 3x^2 - x - 5\) by \(x - 1\)
Post a Comment
Click here to read more

Previous year question paper

Maths PYQs For qualifier exam preparation, complete all your graded assignments and practice assignments for all four weeks, and thoroughly solve 3-4 previous years’ questions (PYQs). This should be more than enough. Many people find math challenging, so I have provided detailed solutions for four PYQs. These questions cover the entire syllabus and include all types of questions. Try to solve them, as it will be very beneficial. Maths Previous Year Questions PYQ1 PYQ2 PYQ3 PYQ4 Maths PYQ Solutions Maths PYQ Detailed Solutions PYQ1 PYQ2 PYQ3 PYQ4 PYQs Statistics1 PYQ1 PYQ2 PYQ3 PYQ4 CT PYQ1 PYQ2 PYQ3 PYQ4 English PYQ1 PYQ2 PYQ3 PYQ4 For quiz 2 and end term Quiz 2 End t
Post a Comment
Click here to read more

Maths 1 week 1 Summary

Number System and Set Theory πŸ“š Set Theory Sets ExplainedπŸ‘‰ Watch here This week, our teacher covered the basics of the number system. We were instructed to consider 0 as part of the natural numbers, as it will be treated as such in future subjects like Python. However, in exams, it will be explicitly stated whether 0 should be considered a natural number. The key topics from this week include set theory and the relationship between two sets. In set theory, we focused on three Venn diagram problems. In the context of relations, we discussed the concepts of reflexive, symmetric, transitive, and equivalence relations. Detailed Explanation 1.Union of Two Sets The union of two sets A and B is the set of elements that are in either A , B , or both. It is denoted as A ∪ B . 2.Intersection of Two Sets The intersection of two sets A and B is the set of elements that are in both A and B . It is denoted as A ∩ B .
Post a Comment
Click here to read more

CT Week 4

Summary πŸ“š Selecting cards: Iterator with filtering This section discusses how to use iterators with filtering to select specific cards from a collection. It involves creating an iterator that can traverse through a collection and apply a filter to select only the desired elements. Examples Total spend of one person This will calculates the total amount spent by a single person. It involves iterating through a list of transactions and summing up the amounts associated with the specified person. Number of verbs This will counts the number of verbs in a given text. It involves iterating through the words in the text and applying a filter to select only the verbs. Sum of both girls’ marks and boys’ marks This will calculates the total marks obtained by girls and boys separately. It involves iterating through a list of students' marks and summing up the marks based on gender. Total revenues of each shop This will calculates the total revenu
Post a Comment
Click here to read more

Maths 1 week 2 Summary

Coordinate Geometry Formulas πŸ“š Coordinate Geometry Formulas Distance Formula Between Two Points Explanation: Calculates the distance between two points \((x_1, y_1)\) and \((x_2, y_2)\). Formula: \(d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\) Section Formula Explanation: Determines the coordinates of a point dividing a line segment internally in the ratio \(m:n\). Formula: \(\left(\frac{mx_2 + nx_1}{m+n}, \frac{my_2 + ny_1}{m+n}\right)\) Area of Triangle When Three Coordinates Given Explanation: Calculates the area of a triangle with vertices at \((x_1, y_1)\), \((x_2, y_2)\), and \((x_3, y_3)\). Formula: \(\text{Area} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right|\) Parallel Lines Explanation: Lines with the same slope. Formula: If \(m_1 = m_2\), the lines ar
Post a Comment
Click here to read more

Statistics 1 Week 4

Statistical Concepts πŸ“š Statistical Concepts Summary and Association Between Two Categorical Variables When analyzing the relationship between two categorical variables, we often use a contingency table. This table displays the frequency distribution of the variables, allowing us to observe any potential association between them. Contingency Table A contingency table, also known as a cross-tabulation or crosstab, is a matrix format that displays the frequency distribution of variables. Each cell in the table represents the frequency count of occurrences for a specific combination of the variables. | | Category 1 | Category 2 | Total | |-----------|------------|------------|-------| | Variable A| 10 | 20 | 30 | | Variable B| 15 | 25 | 40 | | Total | 25 | 45 | 70 | Row
Post a Comment
Click here to read more

Supplementary content

Book Collection Marking pattern in exam: Suppose one question is worth 6 marks and there are three correct options, say B, D, and E. Then each option will be worth 2 marks. If you mark only B and D, you will get 4 marks. If you mark any incorrect option, say B, C, D, you will get 0 marks as C was the wrong answer. So if you are not sure of the option, better don’t mark it, or else you will end up getting 0 marks. πŸ‘‡ Supplementary Material Provided by Instructor Student book Spending some time reading it will be highly beneficial. Student Book Statistics These two books are written by Prashant sir. These two books are more than enough to cover Statistics 1 week 1 to 12. I have provided a short summary which will help you memorize terms and terminology. If you don't understand, refer to these books. These two books were made available online by IIT Madras, and their dist
Post a Comment
Click here to read more

Maths 1 Week 3 Summary

πŸ“š Quadratic Functions Summary A quadratic function is a polynomial function of degree 2, generally represented as \( f(x) = ax^2 + bx + c \) , where a, b , and c are constants, and a \neq 0 . Graph of Quadratic Function The graph of a quadratic function is a parabola. It can open either upward or downward depending on the sign of the coefficient a . If a > 0 , the parabola opens upward. If a < 0 , it opens downward. Axis of Symmetry The axis of symmetry of a parabola is a vertical line that divides the parabola into two mirror images. It can be found using the formula \( x = -\frac{b}{2a} \) . Coordinates of the Vertex The vertex of the parabola is the highest or lowest point on the graph, depending on whether it opens downward or upward. The coordinates of the vertex can be found using the formula \( (x, y) = \left(-\frac{b}{2a}, f\left(-\frac{b}{2a}\right)\right) \) . Parabola Opening Upward and Downwa
Post a Comment
Click here to read more

English Week 1 to 12 summary

Vowels and Consonants πŸ“š Vowels and Consonants English 1 playlist English 2 playlist English Graded Assignment Vowels Vowels are speech sounds produced without any significant constriction or blockage of airflow in the vocal tract. The primary vowels in English are a, e, i, o, u , and sometimes y . Consonants Consonants are speech sounds produced with some degree of constriction or closure at one or more points along the vocal tract. The consonants in English include b, c, d, f, g, h, j, k, l, m, n, p, q, r, s, t, v, w, x, y, z . Sounding Vowels and Consonants Sounding vowels are produced with an open vocal tract, allowing the air to flow freely. Examples include the sounds in "cat" (/Γ¦/), "see" (/iː/), and "moon" (/uː/). Sounding consonants involve some form of obstruction in the vocal tract. For example, the sound /b/ in "bat" involves closing the lips, w
Post a Comment
Click here to read more