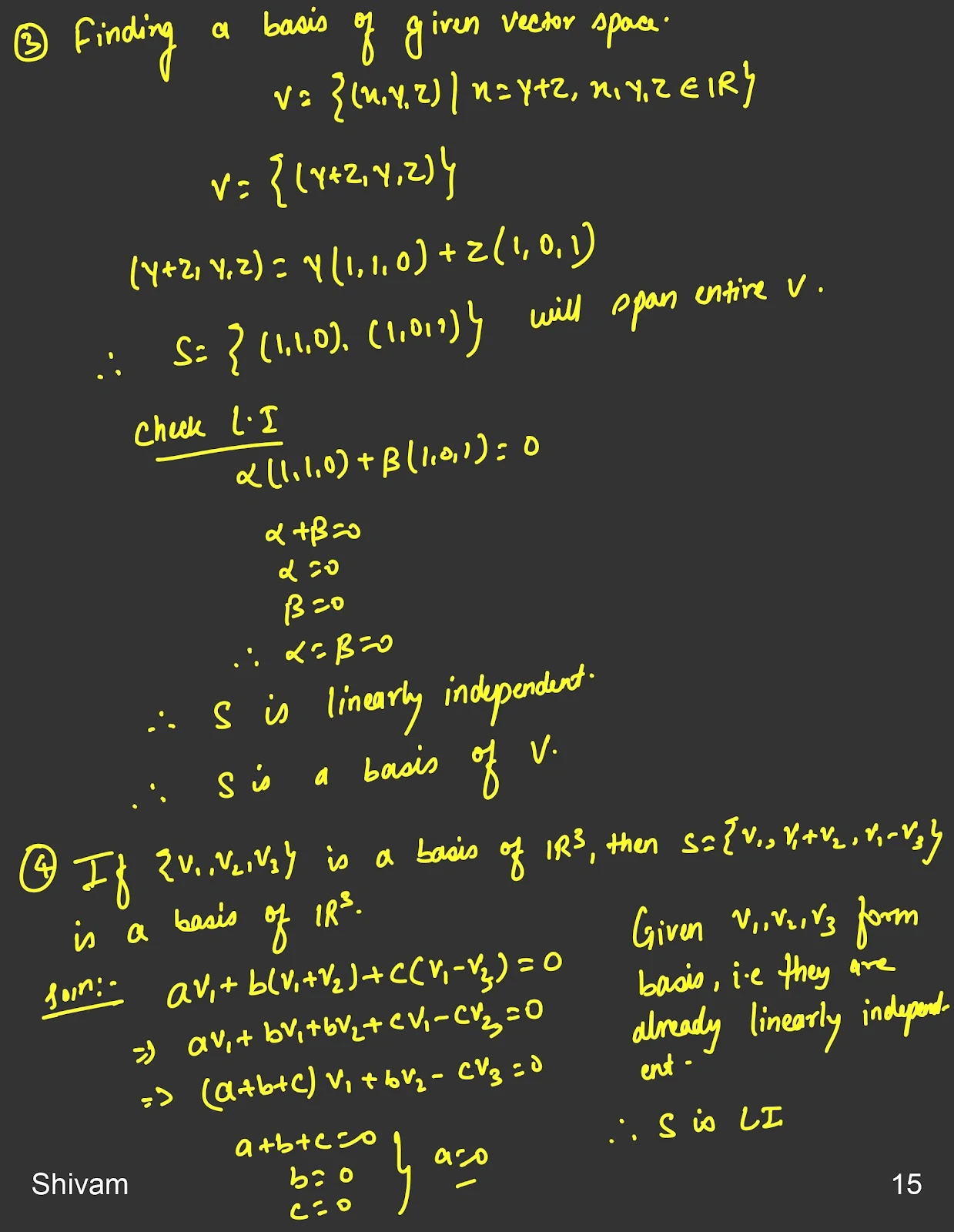Understanding Linear Algebra Concepts: Span, Basis, Dimension, and Rank
1. Span of a Set of Vectors
The span of a set of vectors refers to the set of all possible vectors that can be formed by taking linear combinations of the given vectors. A linear combination means multiplying each vector by a scalar and then adding the results together.
Example:
Consider the set of vectors { v₁ = (1, 0), v₂ = (0, 1) } in R² (2D space). The span of these vectors is the entire 2D plane because any vector (x, y) in R² can be written as:
(x, y) = x(1, 0) + y(0, 1)
2. Spanning Set
A spanning set is a set of vectors that can be combined in all possible ways to reach any vector in the space. If a set of vectors can cover the entire space, it is called a spanning set for that space.
Example:
The set { (1, 0), (0, 1) } spans R² because any vector (x, y) in the 2D space can be formed using these two vectors:
(x, y) = x(1, 0) + y(0, 1)
3. Basis
A basis is a set of linearly independent vectors that also span the entire vector space. These vectors are special because they not only form the entire space but also cannot be written as a combination of each other (they are independent).
Example:
In R³ (3D space), the set { (1, 0, 0), (0, 1, 0), (0, 0, 1) } forms a basis because:
- These vectors are independent: none can be formed by combining the others.
- They span the entire 3D space because any vector
(x, y, z)inR³can be written as:
(x, y, z) = x(1, 0, 0) + y(0, 1, 0) + z(0, 0, 1)
4. Dimension
The dimension of a vector space is the number of vectors in a basis for that space. It tells us how many independent directions exist in the space.
Example:
The dimension of R² (2D space) is 2 because we need two vectors, like { (1, 0), (0, 1) }, to describe the entire space.
The dimension of R³ (3D space) is 3 because three vectors, like { (1, 0, 0), (0, 1, 0), (0, 0, 1) }, are needed to describe the entire space.
5. Finding the Basis of a Set of Vectors
To find the basis of a set of vectors, the vectors must be linearly independent and span the space. If they are not independent, we need to remove the dependent vectors.
- Step 1: Put the vectors into a matrix (either row-wise or column-wise).
- Step 2: Use row reduction (Gauss-Jordan elimination) to simplify the matrix to its row echelon form.
- Step 3: The non-zero rows or columns after reduction represent the basis for the space.
Example:
Consider the set of vectors S = { (1, 2), (2, 4), (3, 6) }. Here's how to find the basis:
- Step 1: Create the matrix with the vectors:
A =
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
A =
| 1 | 2 |
| 0 | 0 |
| 0 | 0 |
(1, 2) is the basis for this set, so the basis is:
{ (1, 2) }
6. Rank of a Matrix
The rank of a matrix is the maximum number of linearly independent rows or columns in the matrix. It tells you how many dimensions the matrix can span.
Example 1:
Consider the matrix:
A =
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
Step 1: Perform row reduction:
A =
| 1 | 2 |
| 0 | 0 |
| 0 | 0 |
Step 2: The rank is the number of non-zero rows. Here, the rank is 1.
Example 2:
Consider the matrix:
B =
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 1 | 0 |
After row reduction:
B =
| 1 | 0 | 1 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
Step 2: The rank is 2 because there are 2 non-zero rows.