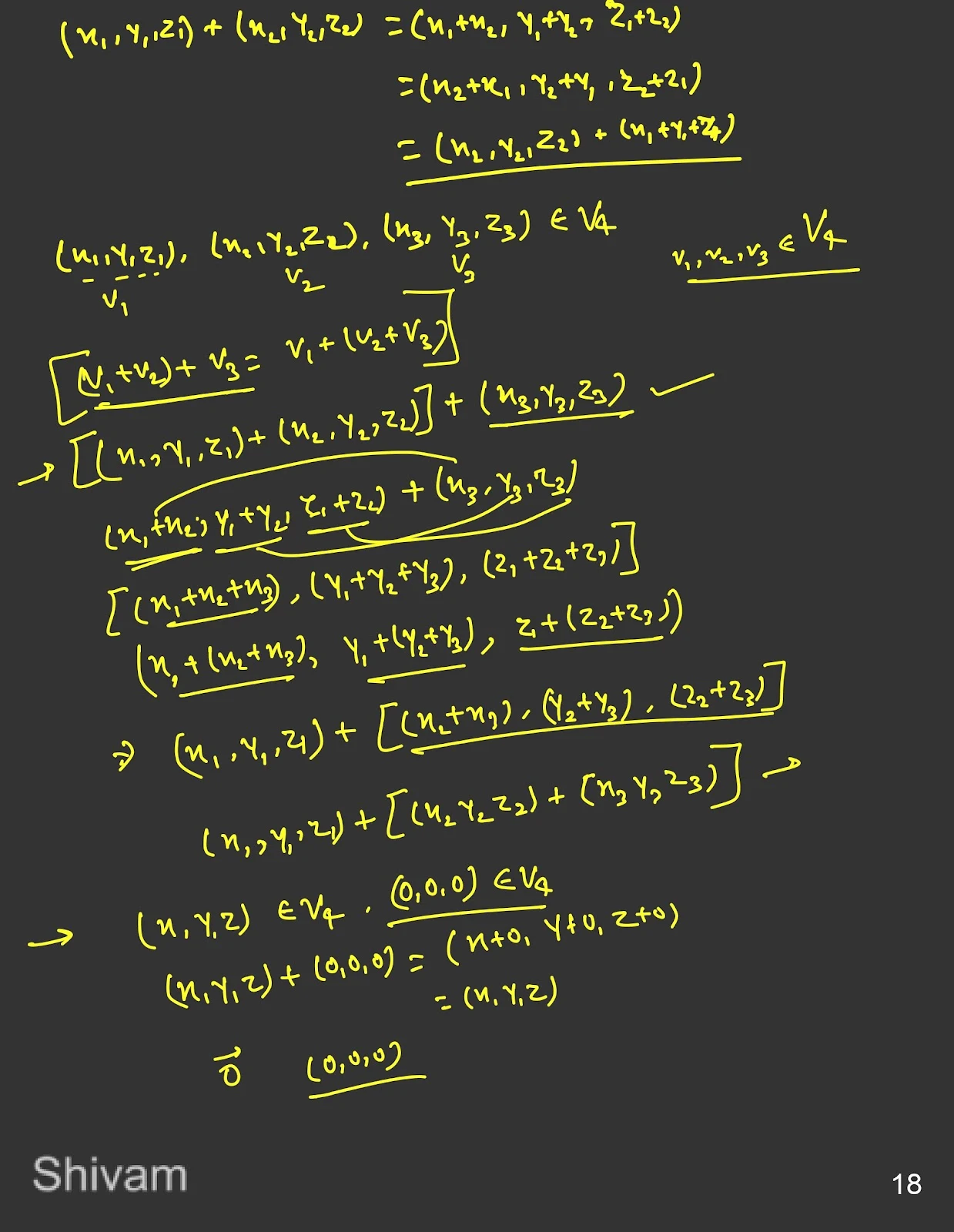Maths 2 Week 3

Understanding Vector Spaces in Linear Algebra

1. Basics: Set Theory and Boolean Operations

A set is a collection of distinct objects, represented by S. Common set operations include:

• Union ($A\cup B$)
• Intersection ($A\cap B$)
• Complement ($A^{\prime }$)

2. Groups

A group $(G,\ast )$ is a set $G$ with an operation * that satisfies:

• Closure: $\mathrm{\forall }a,b\in G,a\ast b\in G$
• Associativity: $\mathrm{\forall }a,b,c\in G,(a\ast b)\ast c=a\ast (b\ast c)$
• Identity: There exists an element $e\in G$ such that $e\ast a=a\ast e=a$ for all $a\in G$
• Inverse: For each $a\in G$, there exists $b\in G$ such that $a\ast b=e$

3. Rings

A ring $(R,+,\cdot )$ is a set equipped with two operations (addition and multiplication) satisfying:

• Closure under addition and multiplication
• Additive associativity
• Multiplicative associativity
• Additive identity (0)
• Distributive properties of multiplication over addition

4. Fields and Their Properties

A field $F$ is a set with two operations (addition and multiplication) that satisfies all ring properties and:

• Multiplicative identity (1)
• Multiplicative inverses: For each $a\ne 0$ in $F$, there exists $a^{-1}\in F$ such that $a\cdot a^{-1}=1$
• Example fields: $\mathbb{R},\mathbb{Q},\mathbb{C}$

Our syllabus starts here: with the concept of a *vector space*. While Groups, Rings, and Fields belong to abstract algebra, understanding Fields is essential for defining vector spaces. A vector space uses elements from a Field, allowing us to perform addition, subtraction, multiplication, and division (except by zero) with predictable behavior. By combining elements from a Field with operations like vector addition and scalar multiplication, we create the structure known as a *vector space*, which forms the foundation of linear algebra. This is where our exploration of linear transformations, solutions to linear equations, and higher-dimensional spaces begins.

👉5. Vector Spaces and Field Interaction

A vector space $V$ over a field $F$ consists of elements called vectors that can be scaled by elements from $F$. The axioms for a vector space include:

Vector Space Axioms

A vector space $V$ over a field $F$ must satisfy the following eight axioms:

1. Closure under Addition: For all $u,v\in V$, the sum $u+v$ is also in $V$.
2. Closure under Scalar Multiplication: For all $c\in F$ and $v\in V$, the product $c\cdot v$ is also in $V$.
3. Associativity of Vector Addition: For all $u,v,w\in V$, $(u+v)+w=u+(v+w)$.
4. Commutativity of Vector Addition: For all $u,v\in V$, $u+v=v+u$.
5. Existence of Additive Identity: There exists an element $0\in V$ such that $v+0=v$ for all $v\in V$.
6. Existence of Additive Inverses: For each $v\in V$, there exists an element $-v\in V$ such that $v+(-v)=0$.
7. Distributive Property of Scalar Multiplication with Respect to Vector Addition: For all $c\in F$ and $u,v\in V$, $c\cdot (u+v)=c\cdot u+c\cdot v$.
8. Distributive Property of Scalar Multiplication with Respect to Field Addition: For all $c,d\in F$ and $v\in V$, $(c+d)\cdot v=c\cdot v+d\cdot v$.
9. Associativity of Scalar Multiplication: For all $a,b\in F$ and $v\in V$, $(a\cdot b)\cdot v=a\cdot (b\cdot v)$.
10. Multiplicative Identity: For all $v\in V$, $1\cdot v=v$, where $1$ is the multiplicative identity in $F$.

6. Examples of Vector Spaces: ${\mathbb{R}}^2$ and ${\mathbb{R}}^3$

In ${\mathbb{R}}^2$ and ${\mathbb{R}}^3$, vectors are ordered pairs or triples, respectively:

• In ${\mathbb{R}}^2$: $\mathbf{v}=\left(\begin{array}{c}x\\ y\end{array}\right)$
• In ${\mathbb{R}}^3$: $\mathbf{v}=\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$

👉7. Linear Dependence and Independence

Vectors are linearly dependent if one can be written as a combination of others; they are independent otherwise.

Linearly Independent vs Dependent Vectors

1. All Scalars Zero (Trivial Solution)

Independent Vectors: If the only solution to the linear combination of vectors being equal to the zero vector is when all the scalars are zero, then the vectors are linearly independent.

Dependent Vectors: If there exists a non-trivial solution where some scalars (other than zero) result in the linear combination being the zero vector, the vectors are linearly dependent.

Example: Vectors v1 = (1, 2) and v2 = (2, 4) are dependent because v2 is a scalar multiple of v1 (i.e., v2 = 2 × v1).

2. At Least One Scalar is Non-Zero (Dependent)

Dependent Vectors: If there is a way to express one vector as a linear combination of others (where at least one scalar is non-zero), the vectors are linearly dependent.

Independent Vectors: If no vector in the set can be written as a linear combination of the others, all the scalars in the linear combination must be zero for the result to be the zero vector.

Example: Vectors v1 = (1, 2) and v2 = (2, 4) are dependent because v2 = 2 × v1.

3. Matrix Rank is Less than the Number of Vectors (Rank Method)

Dependent Vectors: If you create a matrix using the given vectors as columns (or rows) and the rank of this matrix is less than the number of vectors, the vectors are linearly dependent.

Independent Vectors: If the rank of the matrix is equal to the number of vectors, the vectors are linearly independent.

Example: For vectors v1 = (1, 2) and v2 = (2, 4), the matrix formed by placing these vectors as columns is:

A = 
[1  2] 
[2  4]

The rank of the matrix is 1 (less than the number of vectors, which is 2), indicating the vectors are dependent.

4. Determinant of the Matrix (For Square Matrices)

Dependent Vectors: If you form a square matrix from the vectors and the determinant of that matrix is zero, the vectors are linearly dependent.

Independent Vectors: If the determinant of the matrix is non-zero, the vectors are linearly independent.

Example: For vectors v1 = (1, 2) and v2 = (2, 4), the determinant of the matrix:

A = 
[1  2] 
[2  4]

is det(A) = (1 × 4) - (2 × 2) = 0, indicating the vectors are dependent.

5. Geometrical Interpretation

Independent Vectors: If the vectors span a space that has the same dimension as the number of vectors, they are linearly independent. In a 2D plane, two independent vectors will form a non-zero area of the parallelogram they define.

Dependent Vectors: If the vectors lie along the same line or in the same plane (when in 3D), they are dependent. In this case, no new dimensions are added by the vectors.

Example: Two vectors in 2D that are not parallel (not scalar multiples) are independent. Two vectors in 3D that lie on the same plane or line are dependent.

👉Subspaces and Their Axioms

A subspace is a subset of a vector space that is itself a vector space, with the same addition and scalar multiplication operations. For a subset $W\subseteq V$ to be a subspace of the vector space $V$, it must satisfy the following conditions:

Subspace Axioms

1. Non-emptiness: $W$ must contain the zero vector $0$ from $V$. This ensures that $W$ is non-empty and includes an additive identity.
2. Closure under Addition: For any vectors $u,v\in W$, their sum $u+v$ must also be in $W$. This ensures that vector addition remains within the subset.
3. Closure under Scalar Multiplication: For any vector $v\in W$ and any scalar $c$ from the field $F$ (associated with $V$), the product $c\cdot v$ must also be in $W$. This ensures that scalar multiplication keeps the vector in the subset.

Why These Axioms?

If a subset $W$ meets these three conditions, it inherits all the other properties of a vector space automatically. These three conditions make sure that $W$ is closed under the vector space operations, which allows it to be a valid subspace.

Example of a Subspace

In ${\mathbb{R}}^3$, the space of all 3-dimensional vectors, the set of all vectors lying on a plane through the origin is a subspace of ${\mathbb{R}}^3$. This set meets all three subspace conditions: it includes the zero vector, is closed under addition, and is closed under scalar multiplication.

2D Vector Space with a Subspace

In this 2D vector space, the red line through the origin represents a 1D subspace.

]