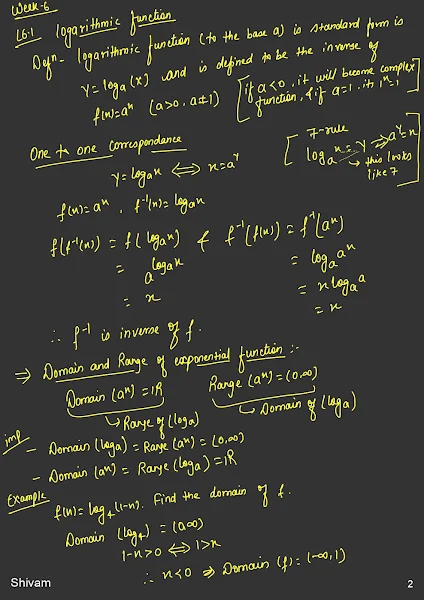📚

Exponential and Logarithmic Functions

Exponential Functions

An exponential function is a mathematical function of the form \( f(x) = a \cdot b^x \), where:

\( a \) is a constant,
\( b \) is the base of the exponential, and
\( x \) is the exponent.

Properties of Exponential Functions:

Domain: The domain of an exponential function is all real numbers, \( (-\infty, \infty) \).
Range: The range is \( (0, \infty) \) for \( b > 1 \) and \( (-\infty, 0) \) for \( 0 < b < 1 \).
Codomain: The codomain is typically all real numbers, but the actual range depends on the function's specific form.
Growth and Decay: If \( b > 1 \), the function represents exponential growth. If \( 0 < b < 1 \), it represents exponential decay.

Example:

Population Growth: If a population of bacteria doubles every hour, the population at time \( t \) hours can be modeled by \( P(t) = P_0 \cdot 2^t \), where \( P_0 \) is the initial population.

Logarithmic Functions

A logarithmic function is the inverse of an exponential function and is of the form \( f(x) = \log_b(x) \), where:

\( b \) is the base of the logarithm,
\( x \) is the argument of the logarithm.

Properties of Logarithmic Functions:

Domain: The domain is \( (0, \infty) \).
Range: The range is all real numbers, \( (-\infty, \infty) \).
Codomain: The codomain is typically all real numbers.
Inverse Relationship: The logarithmic function \( \log_b(x) \) is the inverse of the exponential function \( b^x \).

Example:

pH Levels: The pH level of a solution is calculated using the logarithm: \( \text{pH} = -\log_{10}[\text{H}^+] \), where \( [\text{H}^+] \) is the concentration of hydrogen ions.

Inverse Functions

The inverse of an exponential function \( y = b^x \) is a logarithmic function \( x = \log_b(y) \), and vice versa.

Example:

Solving for Time: If you have an exponential growth model \( P(t) = P_0 \cdot e^{kt} \) and you want to solve for \( t \), you would use the natural logarithm: \( t = \frac{\ln(P/P_0)}{k} \).

Domain and Range

Exponential Functions:

Domain: All real numbers, \( (-\infty, \infty) \).
Range: \( (0, \infty) \) for \( b > 1 \) and \( (-\infty, 0) \) for \( 0 < b < 1 \).

Logarithmic Functions:

Domain: \( (0, \infty) \).
Range: All real numbers, \( (-\infty, \infty) \).

Codomain

The codomain of both exponential and logarithmic functions is typically all real numbers, but the actual range depends on the specific function.

Logarithmic Formulas

Product Rule: \( \log_b(xy) = \log_b(x) + \log_b(y) \)
Quotient Rule: \( \log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y) \)
Power Rule: \( \log_b(x^y) = y \cdot \log_b(x) \)
Change of Base Rule: \( \log_b(x) = \frac{\log_k(x)}{\log_k(b)} \)

Special Explanation of Change of Base Rule:

The change of base rule allows you to convert a logarithm of any base \( b \) to a logarithm of another base \( k \). This is particularly useful when you need to calculate logarithms on a calculator that only supports base 10 or base \( e \) (natural logarithm).

Examples of Logarithmic Functions in Daily Life

Earthquake Magnitude: The Richter scale measures the magnitude of earthquakes using a logarithmic scale. An earthquake that measures 7 on the Richter scale is ten times more powerful than one that measures 6.
Sound Intensity: Decibels (dB) measure sound intensity logarithmically. A sound that is 10 dB louder is perceived as twice as loud.
Information Theory: Logarithms are used to measure information entropy, which quantifies the amount of uncertainty or information content.