Maths 1 week 5 Summary

📚

Functions in Mathematics

A function is a relation between a set of inputs and a set of permissible outputs. It assigns each input exactly one output. Functions are fundamental in mathematics and are used to model real-world phenomena.

Types of Functions

Functions can be classified based on various criteria:

• One-to-One Function (Injective Function): A function f: A → B is one-to-one if different elements in A map to different elements in B. Formally, if f(a1) = f(a2) implies a1 = a2.
• Many-to-One Function: A function where two or more elements in the domain map to the same element in the codomain.
• Onto Function (Surjective Function): A function f: A → B is onto if every element in B is the image of at least one element in A.
• Bijective Function: A function that is both one-to-one and onto. It establishes a perfect "pairing" between the elements of the domain and codomain.

Domain, Codomain, and Range

The domain of a function is the set of all possible inputs. The codomain is the set of all potential outputs, while the range is the set of actual outputs.

Composite Function

A composite function is formed when one function is applied to the result of another function. If f and g are functions, the composite function is denoted as (f ∘ g)(x) = f(g(x)). The domain of the composite function is the set of all x in the domain of g such that g(x) is in the domain of f.

Exponential Function

An exponential function is of the form f(x) = a^x, where a is a positive constant. These functions are characterized by rapid growth or decay.

Logarithmic Function

A logarithmic function is the inverse of an exponential function and is of the form f(x) = log_a(x), where a is the base of the logarithm.

Trigonometric Functions

Trigonometric functions relate angles to the ratios of sides in a right triangle. The primary trigonometric functions are sine (sin), cosine (cos), and tangent (tan).

Floor and Ceiling Functions

The floor function, denoted as ⌊x⌋, maps a real number to the largest integer less than or equal to x. The ceiling function, denoted as ⌈x⌉, maps a real number to the smallest integer greater than or equal to x.

Modulus Function

The modulus function, denoted as |x|, returns the absolute value of x, which is the non-negative value of x without regard to its sign.

Horizontal and Vertical Line Tests

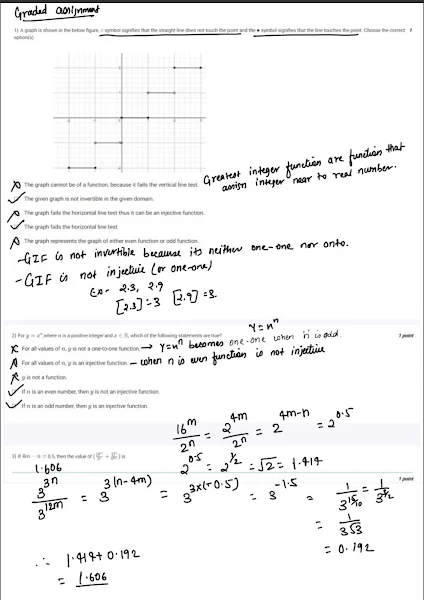
The vertical line test is used to determine if a graph represents a function. If any vertical line intersects the graph at more than one point, it is not a function. The horizontal line test is used to determine if a function is one-to-one. If any horizontal line intersects the graph at more than one point, the function is not one-to-one.

Sensitivity of Function

Sensitivity of a function refers to how the output of the function changes with respect to changes in the input. This is often analyzed using derivatives in calculus.

Conclusion

Understanding the different types of functions and their properties is crucial in mathematics. Functions are used to model and solve real-world problems, making them an essential concept in various fields.

Click on the function

y = x

y = 2^x

y = 0.2^x

y = log(x)

y = sin(x)

y = cos(x)

y = |x|

y = floor(x)

Function

Here are some mathematical formulas written using MathJax:

One-to-One Function: \( f(x_1) = f(x_2) \implies x_1 = x_2 \)

Composite Function: \( (f \circ g)(x) = f(g(x)) \)

Exponential Function: \( f(x) = a^x \)

Logarithmic Function: \( f(x) = \log_a(x) \)

Trigonometric Functions: \( \sin(x), \cos(x), \tan(x) \)

Floor Function: \( \lfloor x \rfloor \)

Ceiling Function: \( \lceil x \rceil \)

Modulus Function: \( f(x) = |x| \)